عنوان فصل اول: راهبرد تقريبهاي متوالي و شناخت اعداد حقيقي
نقشه هاي مفهومي در برگيرنده محتواي موضوعي رياضي و محتواي فرايندي رياضي ميشود.
محتواي موضوعي – فرايندي اين فصل به صورت زير خواهد بود.
١‐ بخش آغازين
انجام دادن بر اساس » روش درست يادگيري و فهميدن رياضيات با تمركز بر سه انديشة محوری استوار شده است. « معنا و مفهوم فهميدن و يادگيري در رياضيات » و « تفكربر پاية انجام دادن » ، « تفكریك بيان كلي معناي دانايي در رياضي ارائه ميشود:
« در رياضيات، دانستن يعني توانايي انجام دادن »
نقشه مفهومي كلي؛ بخش اول :- concept maps
فهميدن و يادگيري دررياضيات
پنداشتهاي نادرست يا بدفهمي ها
انجام دادن براساس تفكر ديدن، شنيدن،خواندن تفكر براساس انجام دادن
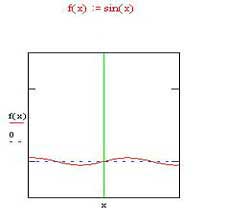
در اين قسمت مفاهيم معادلة و تابع درجة ٢، تابع سينوس و لگاريتم، تركييب توابع، مفهوم مشتق و قوانين مشتق گيري به عنون ابزار و مواد رياضي به كار گرفته ميشوند.
شامل باورها نسبت به ياددهي– (Belief System) ! هدف بنيادي بخش نخست: اصلاح نظام باورها
يادگيري رياضيات و باورهاي مربوط به موضوع رياضيات.
چند انديشه اساسي حاكم بر فصل اول:
الف‐ رويكرد فرهنگي‐ تربيتي مبتني بر فرهنگ اسلامي‐ ايراني. اين رويكرد براساس اسناد پژوهشي رسمي وزارت آموزشو پرورش پيرامون اين موضوع شكل گرفته است. در حوزة علمي آموزش رياضي از رويكردهاي فرهنگ مدار مبتني بر نظريه ويگوتسكي استفاده ميشود. (براي پياده سازي اين رويكرد ازمنابع دورة تمدن اسلامي با محوريت ا يران استفاده شده است.
ب‐ از مدلهاي آموزشي – تعليمي سه مرحله اي و پنج مرحله اي براي سازماندهي ساختارمتن استفاده شده است.
پ‐ راهبرد تقريبهاي متوالي و مهارت تقريب زدن به عنوان زيرساخت و بستر ياددهي‐ يادگيري اين فصل قرار دارند، بنابراين ميتوان آنها را از اهداف محتواي فرايندي – مهارتي برنامه ريزي شدة اين فصل قلمداد كرد. به علاوه مهارت تعميم دادن نيز از اهداف محتواي فرايندي‐مهارتي برنامه ريزي شدة اين فصل است.
ت‐ سازماندهي محتوا و ساختار متن بر پاية فعاليتهاي فكري رياضي، بحث گروهي و ارائه دركلاس شكل گرفته است.
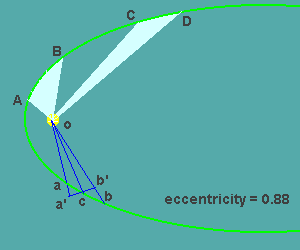
تقريب زدن π روش غياثالدين جمشيد كاشاني دربارة تقريب زدن عدد محيط و مساحت دايره محور قرار ميگيرد و با روش ارشميدس به طور موازي و گام به گام مقايسه ميشود.
نقشة مفهومي بخش دوم:
دقت/تقريب
نياز به استدلال
دايره، چندضلعي محيطي و محاطي،
قضيه فيثاغورس
قضيه اصلي تشابه ارشميدس
قضيه اصلي كاشاني
انديشه و راهبردتعميم دادن
دنباله و رابطه بازگشتي
راهبرد/ تقريبهاي متوالي
انديشة قضيه ساندويچي
مقايسه كار كاشاني و ارشميدس
راهبردهاي حدس وآزمايش، الگويابي،مدلسازي، جدول نظام دار
تقريبزدن٣√ و Л
تقريب عدد محيط و مساحت دايره
بسط اعشاري اعداد حقيقي
گوياها/ گنگها/چگال بودن
е تقريب زدن
محاسبة خطا
نابرابريها،قدر مطلق
مهارت مقايسه كردن
٣‐ قسمت پاياني فصل): موضوعات بسط اعشاري اعداد حقيقي، دقت و تقريب، محاسبه خطا، نيازبه استدلال با پرداختن به گوياها، گنگها و مفهوم چگال بودن محور قرار ميگيرد ونابرابريها درگيرميشوند.
نقشة مفهومي بخش سوم:
بسط اعشاري اعداد حقيقي
دقت/ تقريب
محاسبه خطا
چگال بودن اعداد گنگ در اعداد حقيقي
خواص قدر مطلق
نابرابريها
استدلال و اثبات
تقريبا عداد گنگ با اعداد گويا
+ نوشته شده در پنجشنبه نهم تیر ۱۳۹۰ ساعت 16:53 توسط سیروس نادریان
|
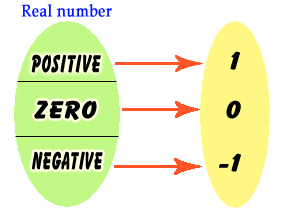
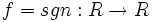 با ضابطه زیر را تابع علامت می گوییم:
با ضابطه زیر را تابع علامت می گوییم: 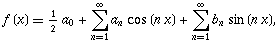
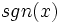 نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است.
نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است. 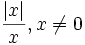
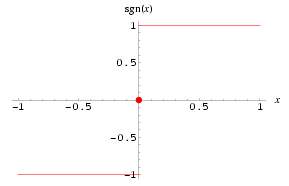
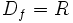 و برد این تابع برابر است با:
و برد این تابع برابر است با: 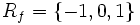 .
. 
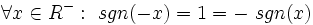
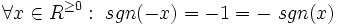
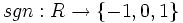 تابعی غیر یک به یک است.
تابعی غیر یک به یک است. 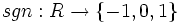
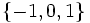 است(چرا؟).
است(چرا؟). 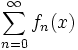 که جمله عمومی آن
که جمله عمومی آن 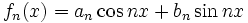
 و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و  ی را نشان میدهد.
ی را نشان میدهد. 
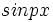 یا
یا 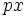 که در آنها p
که در آنها p 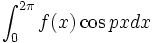 و
و 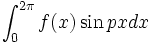
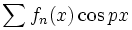 یا
یا 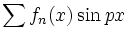 محاسبه کرد
محاسبه کرد 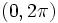 توابع
توابع 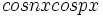 و
و 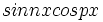 و
و 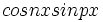 و
و 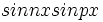 اند.
اند. 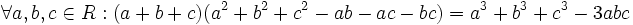

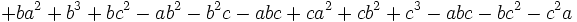
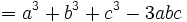
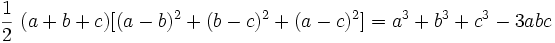
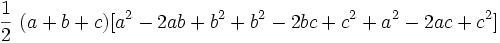
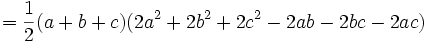
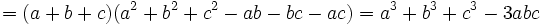
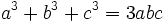

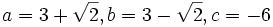 باشد آنگاه داریم:
باشد آنگاه داریم:

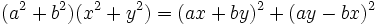
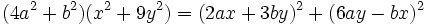
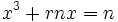 میباشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را میتوان به صورت گفته شده کاهش داد.
میباشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را میتوان به صورت گفته شده کاهش داد.
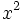 تقسیم میکنیم.
تقسیم میکنیم. 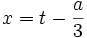 معادله را به فرم زیر تبدیل میکنیم.
معادله را به فرم زیر تبدیل میکنیم. 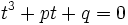
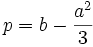 و
و 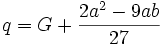 معادله به دست آمده را معادله تقلیل یافته مینامیم.
معادله به دست آمده را معادله تقلیل یافته مینامیم. 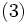
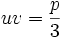
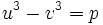
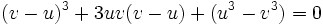
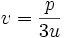
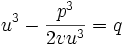
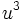 میباشد خواهیم داشت
میباشد خواهیم داشت 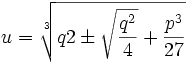 حال چون
حال چون 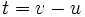 و
و 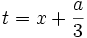 پس
پس 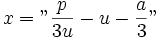
 اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است.
اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است.  با کمی دقت متوجه میشویم که میتوان یک
با کمی دقت متوجه میشویم که میتوان یک 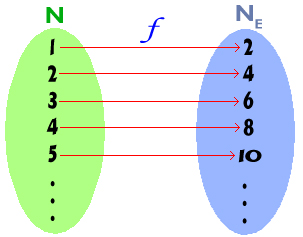
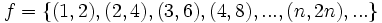 متوجه میشویم
متوجه میشویم 
 را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:
را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم: 
 ،
،  ، که در آنها n عددی طبیعی است.
، که در آنها n عددی طبیعی است. 

.gif)
 در نظر بگيريد . ادعا مي كنيم كه اين ، همان تابع مطلوب است.
در نظر بگيريد . ادعا مي كنيم كه اين ، همان تابع مطلوب است. .gif)



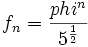
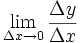
 نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند: 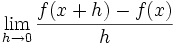
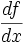 یا
یا 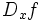 یا
یا 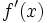
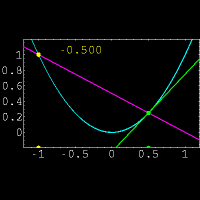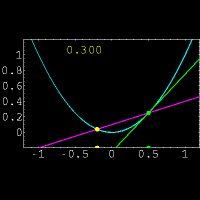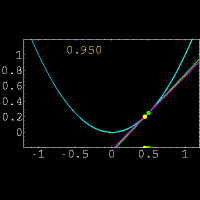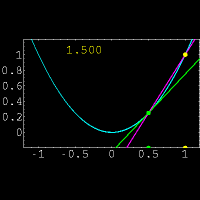
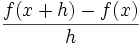
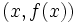 و
و 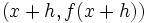 حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ،حاصل حد زیر است:
حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ،حاصل حد زیر است: 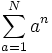

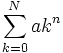
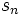 نشان میدهند
نشان میدهند 
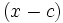 میگویند.واضح است که جملات آن به فرم زیردر میآید
میگویند.واضح است که جملات آن به فرم زیردر میآید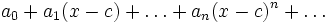
 را میتوان به صورت جمع توابعی بر حسب
را میتوان به صورت جمع توابعی بر حسب  نوشت.
نوشت.