سری تیلور
|
...+5+4+3+2+1 |
سریها بر دو نوعند:سریهای متناهی و نامتناهی؛که سریهای متناهی را می توان با اعمال ساده جبری محاسبه کرد،ولی برای محاسبه سریهای نامتناهی باید از آنالیز کمک گرفت.
به عنوان مثال سری زیر یک سری متناهی است.
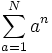
به این سری توجه نمایید:

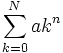
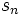 نشان میدهند
نشان میدهند در صورتی که
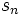 به سمت یک عدد متناهی سیر کند آن را همگرا مینامند. در غیر این صورت به آن یک سری واگرا گویند.
به سمت یک عدد متناهی سیر کند آن را همگرا مینامند. در غیر این صورت به آن یک سری واگرا گویند. حال به معرفی نوع دیگری از سریها به نام سریهای توانی می پردازیم:سریهایی را که جملات آن توابعی از متغیر x باشند را سریهای توانی گویند.و مجموعه مقادیر از x که به ازای آنها توابع موجود در سری تعریف شده و سری همگرا باشد را میدان همگرایی سری گویند. هر سری تابعی به شکل

را یک سری توانی بر حسب 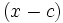 میگویند.واضح است که جملات آن به فرم زیردر میآید
میگویند.واضح است که جملات آن به فرم زیردر میآید
|
|
حال به قضیه مهمی به نام قضیه تیلور میرسیم؛طبق این قضیه میتوان هر تابعی را که در یک بازه بینهایت بار مشتق پذیر باشد میتوان در این بازه به صورت یک سری توانی نامتناهی که به سری تیلور معروف است نشان داد.به عنوان مثال تابعی مانند
 را میتوان به صورت جمع توابعی بر حسب
را میتوان به صورت جمع توابعی بر حسب  نوشت.
نوشت. قبل از اینکه به توضیح کامل درباره این سریها بپردازیم.مثالی را در مورد این سریها بیان میکنیم.تابع sinx را در نظر بگیرید.این تابع را میتوان به صورت سری زیر بیان کرد:
 |
لازم به توضیح است که در سری فوق c=0 در نظر گرفته شده است.
در اشکال زیر نمودار سری به ازای n=4؛ n=7 و نمودار sinx از راست به چپ رسم شده است.
همانطور که مشاهده میشود هر قدر تعداد جملات سری افزایش یابد شکل آن به یک منحنی تبدیل مشود.و اگر تا بینهایت رسم شکل ادامه یابد به شکل تابع sinدر می آید.
 |
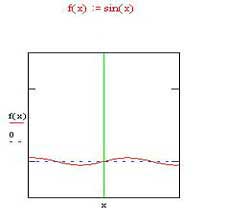
حال به شکل تابع sinx توجه کنید متوجه میشوید که با ادامه روند رسم اشکال به ازای nهای نامتناهی سرانجام به شکل sinx خواهیم رسید.
حال در ادامه به تشریح کامل سریهای تیلور می پردازیم.
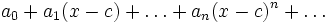














.gif)





















