تابع علامت
تابع 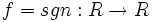 با ضابطه زیر را تابع علامت می گوییم:
با ضابطه زیر را تابع علامت می گوییم:
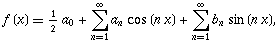
لازم به ذکر است که این تابع را با نماد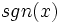 نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است.
نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است.
همچنین ضابطه این تابع را برای X های مخالف صفر می توان اینگونه تعریف کرد: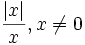
در این تابع دامنه مجموعه اعداد حقیقی است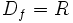 و برد این تابع برابر است با:
و برد این تابع برابر است با: 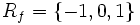 .
.
این تابع از معروف ترین توابع چند ضابطه ای است که نحوه عملکرد آن به این صورت است:
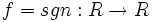 با ضابطه زیر را تابع علامت می گوییم:
با ضابطه زیر را تابع علامت می گوییم: 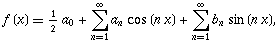
لازم به ذکر است که این تابع را با نماد
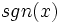 نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است.
نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است. همچنین ضابطه این تابع را برای X های مخالف صفر می توان اینگونه تعریف کرد:
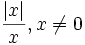
در این تابع دامنه مجموعه اعداد حقیقی است
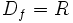 و برد این تابع برابر است با:
و برد این تابع برابر است با: 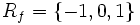 .
. این تابع از معروف ترین توابع چند ضابطه ای است که نحوه عملکرد آن به این صورت است:
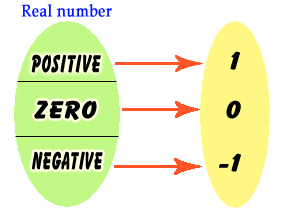
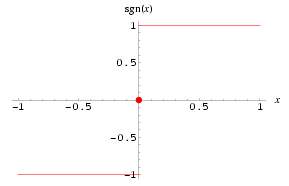
- اگر متغییر x داده شده به تابع مثبت باشد آن را به عدد یک و اگر متغییر x داده شده به تابع منفی باشد آن را به منفی یک متناظر می کند و اگر متغییر داده شده x=0 باشد آن را به عدد صفر متناظر می کند. به عبارت دیگر این تابع هر عدد حقیقی مثبت را به یک، هر عدد حقیقی منفی را به منفی یک متناظر می کند و عدد صفر را هم به صفر متناظر می کند.
- نمودار پیکانی زیر نحوه عملکرد تابع علامت(sgn) را نشان می دهد:

- با توجه به ضابطه این تابع نمودار آن به این صورت خواهد بود:

- بررسی ویژگی های تابع علامت
- تابع علامت تابعی فرد است.
برهان: تابع 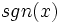 را در نظر بگیرید:
را در نظر بگیرید:
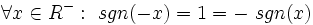
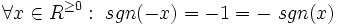
که این نشان می دهد این تابع فرد است. همچنین نمودار این تابع نسبت به مبدا مختصات متقارن است که دلیل بر فرد بودن تابع است.
 را در نظر بگیرید:
را در نظر بگیرید: 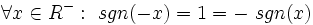
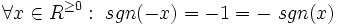
که این نشان می دهد این تابع فرد است. همچنین نمودار این تابع نسبت به مبدا مختصات متقارن است که دلیل بر فرد بودن تابع است.
- تابع علامت
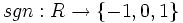 تابعی غیر یک به یک است.
تابعی غیر یک به یک است.
برهان: در توابع چند ضابطه ای شرط اولیه برای یک به یک بودن تابع این است که هر ضابطه یک به یک باشد اما مشاهدی می شود در مورد تابع علامت این شرط برقرار نمی باشد. پس این تابع یک به یک نمی باشد.
- تابع علامت
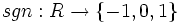 تابع پوشا است.
تابع پوشا است.
برهان: می دانیم در بررسی پوشا بودن توابع چند ضابطه ای به این صورت عمل می کنیم که برد هر ضابطه را محاسبه کرده اجتماع آنها را بدست می آوریم. اگر حاصل با مجموعه انجام تابع برابر باشد تابع پوشا است. حال در تابع علامت اجتماع بردهای هر ضابطه برابر با مجموعه 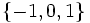 است(چرا؟).
است(چرا؟).
و چون با مجموعه انجام تابع یعنی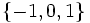 برابر است پس این تابع پوشا است.
برابر است پس این تابع پوشا است.
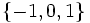 است(چرا؟).
است(چرا؟). و چون با مجموعه انجام تابع یعنی
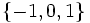 برابر است پس این تابع پوشا است.
برابر است پس این تابع پوشا است.
+ نوشته شده در جمعه یازدهم آذر ۱۳۹۰ ساعت 8:45 توسط سیروس نادریان
|
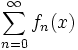 که جمله عمومی آن
که جمله عمومی آن 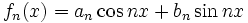
 و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و  ی را نشان میدهد.
ی را نشان میدهد. 
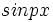 یا
یا 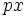 که در آنها p
که در آنها p 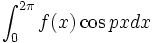 و
و 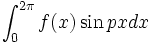
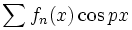 یا
یا 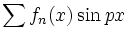 محاسبه کرد
محاسبه کرد 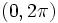 توابع
توابع 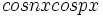 و
و 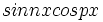 و
و 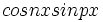 و
و 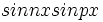 اند.
اند. 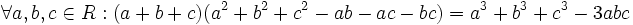

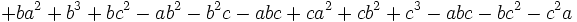
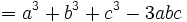
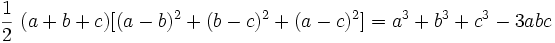
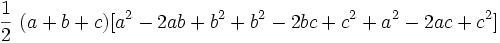
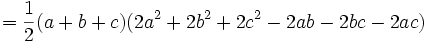
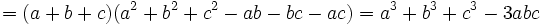
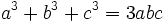

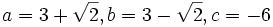 باشد آنگاه داریم:
باشد آنگاه داریم:

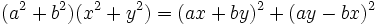
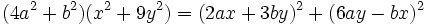
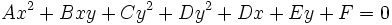
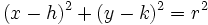
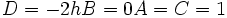
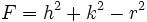 -
- 
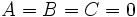 ولی این شرایط معادله درجه دوم را به یک معادله خطی بجای معادله درجه دوم بدل میکنند جملات
ولی این شرایط معادله درجه دوم را به یک معادله خطی بجای معادله درجه دوم بدل میکنند جملات 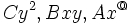 جملات درجه دوم میباشند و در حال حاضر رابطه ذکر شده در تعریف را وقتی که لااقل یکی از این جملات درجه وجود داشته باشند بررسی خواهیم کرد.
جملات درجه دوم میباشند و در حال حاضر رابطه ذکر شده در تعریف را وقتی که لااقل یکی از این جملات درجه وجود داشته باشند بررسی خواهیم کرد. 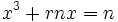 میباشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را میتوان به صورت گفته شده کاهش داد.
میباشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را میتوان به صورت گفته شده کاهش داد.
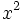 تقسیم میکنیم.
تقسیم میکنیم. 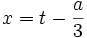 معادله را به فرم زیر تبدیل میکنیم.
معادله را به فرم زیر تبدیل میکنیم. 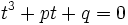
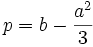 و
و 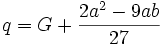 معادله به دست آمده را معادله تقلیل یافته مینامیم.
معادله به دست آمده را معادله تقلیل یافته مینامیم. 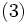
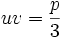
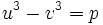
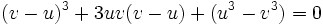
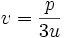
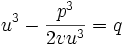
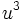 میباشد خواهیم داشت
میباشد خواهیم داشت 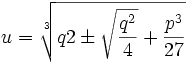 حال چون
حال چون 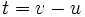 و
و 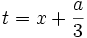 پس
پس 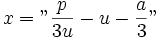
 اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است.
اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است.  با کمی دقت متوجه میشویم که میتوان یک
با کمی دقت متوجه میشویم که میتوان یک 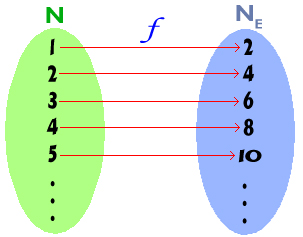
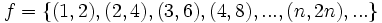 متوجه میشویم
متوجه میشویم 
 را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:
را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم: 
 ،
،  ، که در آنها n عددی طبیعی است.
، که در آنها n عددی طبیعی است. 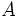 از اعداد صحیح یا حقیقی دارای یک عنصر مینیمم و یک عنصر ماکسیمم است .
از اعداد صحیح یا حقیقی دارای یک عنصر مینیمم و یک عنصر ماکسیمم است .  باشد آنگاه
باشد آنگاه  و اگر
و اگر  آنگاه
آنگاه  .
. 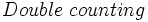 را بررسی کنیم. قبل از هر چیز، لازم است اندکی به خود این روش اشاره کنیم تا آمادگی بیشتری برای درک مسایل حاصل شود؛ همان گونه که از نام این روش پیدا است، ما قرار است که یک کمیت ترکیباتی را از دو روش متفاوت بشماریم و چون این دو روش، یک چیز را می شمارند، طبیعتا با هم برابرند. در وهله اول، شاید این روش، بسیار بدیهی و ساده به نظر آید؛ اما این گونه نیست و بسیاری از مسایل ترکیباتی با استفاده از این روش حل می شوند؛ همان گونه که
را بررسی کنیم. قبل از هر چیز، لازم است اندکی به خود این روش اشاره کنیم تا آمادگی بیشتری برای درک مسایل حاصل شود؛ همان گونه که از نام این روش پیدا است، ما قرار است که یک کمیت ترکیباتی را از دو روش متفاوت بشماریم و چون این دو روش، یک چیز را می شمارند، طبیعتا با هم برابرند. در وهله اول، شاید این روش، بسیار بدیهی و ساده به نظر آید؛ اما این گونه نیست و بسیاری از مسایل ترکیباتی با استفاده از این روش حل می شوند؛ همان گونه که