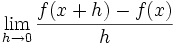اینک یکان نو 18

نشانی وبلاگ مجله
www.yekan.blogfa.com

نشانی وبلاگ مجله
www.yekan.blogfa.com
در ریاضیات شش عدد وجود دارند که از بقیه ی اعداد متمایزند زیرا آنها ویژگی هایی دارند که سایر اعداد ندارند. این اعداد عبارتند از : صفر، یک، پی(نسبت محیط دایره به قطر آن)، e (عدد اویلر)،i (مبنای اعداد مختلط) و فای(نسبت طلایی). اویلر ریاضیدان سویسی قرن هجدهم رابطه ای بین پنج تا از این اعداد را بصورت این معادله کشف کرد:

اگر این معادله را در یک قاب عکس قرار داده و روی دیوار و در کنار تابلوی مونالیزا نصب کنید، در چشم یک ریاضیدان نه تنها هیچ از مونالیزا کم ندارد بلکه میتواند بسیار شگفت انگیز تر هم باشد. مونالیزا را تقریبا" هر کسی به اندازه فهمی که از هنر نقاشی دارد درک میکند و بدیهی است هر چه این فهم عمیق تر و فنی تر باشد، درک هم عمیق تر خواهد بود. اما زیبایی و شگفتی این معادله را تنها کسی میفهمد که با اعداد الفت دراز داشته و بویژه این پنج عدد را شناخته و چگونگی خلقت آنها را فهمیده باشد و بداند که هر چند آنها به ظاهر نزدیک هم اند اما ماهیت آنها به اندازه کهکشانها از یکدیگر دور است ولی وقتی استادانه در کنار هم قرار میگیرند چنان با شوق با یکدیگر می جوشند که تعادلی متقارن و بس زیبا و بدیع بوجود می اورند. تازه این معادله خود حالت خاصی از یک معادله کلی تر، زیبا تر و شگفت انگیز تری است که پای دو نسبت مثلثاتی اصلی را هم به میان میکشد :

همایش سالیانه انجمن معلمان ریاضی استان فارس روز جمعه۳۰/۱۱/۸۸ از ساعت ۹ صبح تا ۱۲ تشکیل می گردد
برنامه های همایش عبارتند از:سخنرانی علمی-ارائه IT -اجرائ برنامه های فرهنگی علمی-کارگاه های آموزشی
از دبیران تمام مقاطع تحصیلی مخصوصا اعضائ انجمن جهت شرکت در این همایش دعوت به عمل می آید.
مکان:مرکز فرهنگی تربیتی اندیشه-شیراز-خیابان زینبیه(مقابل بیمارستان شهید بهشتی)-روبروی بوستان ولی عصر
1-ثابت کنید تمام مردم دنیا دریک اتوبوس جا می گیرند.
اثبات با استقراء ریاضی:
برای n=1 : بدیهی است یک نفر دراتوبوس جا می گیرد.
فرض استقراء : فرض می کنیم برای n=k حکم درست باشد.
باید نشان دهیم برای n=k+1 نیز حکم درست است. یک نفر را جدا می کنیم ، k نفر باقی مانده طبق فرض در اتوبوس جا می گیرند، حال اگر مسافران کمی جا به جا شوند یک نفر به راحتی در اتوبوس جا می شود. بنابراین حکم ثابت است.
2-ثابت كنید تمام اسب های دنیا هم رنگند.
اثبات به استقراء: برای n=1 در مجموعه ای شامل یک عضو بدیهی است.
n=k فرض کنیم در مجموعه ای شامل k اسب، اسب ها همرنگند.
برای n=k+1 ابتدا یکی از اسب ها را بیرون بکشید k اسب باقی مانده بنابر فرض استقراء همرنگند اینک اسب بیرون کشیده شده را بر مجموعه بازگردانده ، اسب دیگری بیرون بیاورید این بار هم k اسب باقی مانده از فرض استقراء همرنگند و حکم ثابت است.
به نظر شما اشكال استدلال های بالا در چیست ؟
آیا تمام مردم دنیا در یك اتوبوس جا می گیرند ؟!
واقعاً تمام اسب های دنیا هم رنگند ؟!
وسایل مورد نیاز
دریل و مته، درفش، مداد، قلم، چاقو، مهره، پیچ، پونز بزرگ، واشر، چوب پنبه، مداد تراش، سنباده، میخ پرچ، خط كش، چوب بالسا، كاتر
١- شما به دو تكه چوب بالسا به ابعاد ۲٢*٢ سانتیمتری و دو تكه ١٢*٢ سانتیمتری نیاز دارید.
٢- به كمك سنباده انتهای چوب های بالسا را به شكل نیم دایره صاف كنید. 
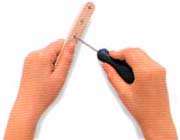
٣- پنج نقطه متساوی الفاصله در طول هر تكه اندازه گرفته (یكی از آنها دقیقاً در انتهاء باشد) و محلی را كه باید سوراخ شود را با * مشخص كنید.سپس در هر علامت، سوراخی ایجاد كنید.
٤- هر یك از بازوهای كوچك را به میانه هر یك از بازوهای بلند وصل كنید. پیچی از آن عبور داده، سپس یك مهره به طرف دیگر پیچ بیاندازید و در پایان آن را با مهره ببندید.

٥- یك سوراخ در مركز چوب پنبه ایجاد كنید. مدادی از آن رد كرده، سپس از سوراخ های انتهایی بازوهای كوچك عبور دهید.

٦- قطعه چوبی را با مداد تراش تیز كنید. این وسیله اشاره گر شما است. اشاره گر را از سوراخ انتهایی بازوی راست عبور دهید.

٧- اشاره گر را روی شكل قرار دهید. ورق كاغذی را زیر مداد بگذارید. پونز بزرگی را در بازوی چپ قرار دهید. آن را با یك دست بگیرید و شكل اصلی را به كمك اشاره گر دنبال (ردیابی) كنید. قلم چه نوع شكلی را ایجاد می كند؟
خط d را در صفحه در نظر بگيريد. اگر O نقطهي دلخواهي بر d و نقاط![]() به ترتيب قرينهي A,B نسبت به O باشند، آيا ميتوان AB را با حركت دادن روي d بر
به ترتيب قرينهي A,B نسبت به O باشند، آيا ميتوان AB را با حركت دادن روي d بر ![]() منطبق كرد؟
منطبق كرد؟

قطعاً پاسخ منفي است. امّا با دوران AB حول O در صفحه، ميتوان آن را بر![]() منطبق كرد يعني با رفتن به بعدي بالاتر. [ خط يك بعدي و صفحه دو بعدي است]
منطبق كرد يعني با رفتن به بعدي بالاتر. [ خط يك بعدي و صفحه دو بعدي است]
خط d و مربّع ABCD در صفحه مفروضاند. اگر نقاط ![]() به ترتيب قرينهي A,B,C,D نسبت به d باشند، آيا ميتوان ABCD را با حركت دادن در صفحه بر
به ترتيب قرينهي A,B,C,D نسبت به d باشند، آيا ميتوان ABCD را با حركت دادن در صفحه بر![]() منطبق كرد؟
منطبق كرد؟

قطعاً پاسخ منفي است. امّا با دوران ABCD حول d در فضا، ميتوان آن را بر![]() منطبق كرد يعني با رفتن به بعدي بالاتر [صفحه دو بعدي و فضا سه بعدي است]
منطبق كرد يعني با رفتن به بعدي بالاتر [صفحه دو بعدي و فضا سه بعدي است]
اكنون فرض كنيد روبهروي يك آينهي قدّي ايستادهايد و به تصوير و فضاي اطراف خود،در آن مينگريد. سؤال اين است كه آيا با حركت در فضا ميتوانيد بر تصوير آينهاي خود منطبق شويد؟
قطعاً پاسخ منفي است. پس طبق روال فوق بايد به بعد بالاتر برويم، يعني بعد چهارم! امّا فضاي چهاربعدي چگونه است؟
معرّفي فضاي چهاربعدي:
يك چهارتايي مرتب از اعداد حقيقي (x,y,z,t) يك نقطه از فضاي چهاربعدي ناميده ميشود. فضاي چهاربعدي داراي چهار محور مختصات است:

در فضاي چهاربعدي علاوه بر محور مختصات، صفحه ي مختصات نيز داريم؛ اينها صفحاتي هستند كه از دو محور مختصات ميگذرند.
فضاي چهار بعدي داراي 6 صفحه ي مختصات است:

به وضوح هر يك از اين صفحات از دو محور مختصات ميگذرند.
امّا كار به همين جا ختم نميشود، در فضاي چهاربعدي، مجموعهاي چون صفحه ي مختصات سه بعدي نيز داريم و آن عبارت است از مجموعهي نقاطي كه يك مختص آنها صفر و سه مختص ديگر ميتوانند عددي دلخواه باشند. فضاي چهاربعدي داراي چهارصفحهي مختصات سه بعدي است:

به وضوح هر يك از اين صفحات مختصات سه بعدي از سه محور مختصات ميگذرند و محل تلاقي هر دو تاي آنها، يك صفحهي مختصات است.
در اين فضا، فاصلهي بين دو نقطهي ![]() به صورت زير تعريف ميشود:
به صورت زير تعريف ميشود:
![]()
و منظور از يك شكل هندسي، يك مجموعه از نقاط است.
اكنون پس از معرّفي فضاي چهاربعدي، جهت درك بهتر آن، ساختار شكل هندسي سادهاي چون مكعب واحد چهاربعدي را بررسي ميكنيم.
پيش از پرداختن به اين موضوع، بد نيست ساختار مكعب واحد سه بعدي را يك بار مرور كنيم.
مكعب واحد سه بعدي عبارت است از![]() .
.
رأس: رأس اين مكعب عبارت است از نقاطي كه مختصهاي آنها 0 يا 1 هستند. مثلاً (1،0،0) يك رأس اين مكعب است. اين مكعب داراي 8 رأس است.
يال: يال اين مكعب عبارت است از مجموعه ي نقاطي كه دو مختص آنها 0 يا 1 بوده و مختص ديگر بين 0 و 1 تغيير ميكند.
مثلاً ![]() يك يال اين مكعب است. اين مكعب داراي 12 يال است.
يك يال اين مكعب است. اين مكعب داراي 12 يال است.
وجه: وجه اين مكعب عبارت است از مجموعه ي نقاطي كه يك مختص آنها 0 يا 1 بوده و دو مختص ديگر بين 0 و 1 تغيير ميكنند.
مثلاً![]() يك وجه اين مكعب است. اين مكعب داراي 6 وجه است. در شكل زير چگونگي ساختن مكعب واحد سه بعدي با استفاده از مدل گستردهاش را ملاحظه ميكنيد:
يك وجه اين مكعب است. اين مكعب داراي 6 وجه است. در شكل زير چگونگي ساختن مكعب واحد سه بعدي با استفاده از مدل گستردهاش را ملاحظه ميكنيد:

اكنون به بررسي ساختار مكعب واحد چهاربعدي ميپردازيم.
مكعب واحد چهاربعدي عبارت است از![]() .
.
رأس: رأس اين مكعب عبارت است از نقاطي كه مختصهاي آنها 0 يا 1 هستند. مثلاً (1،0،0،0) يك رأس اين مكعب است. اين مكعب داراي 16 رأس است.
يال: يال اين مكعب عبارت است از مجموعهي نقاطي كه سه مختص آنها 0 يا 1 و مختص باقيمانده بين 0 و 1 تغيير ميكند. مثلاً![]() يك يال اين مكعب است.
يك يال اين مكعب است.
اين مكعب 32 يال دارد. [چرا؟]
وجه دو بعدي: وجه دو بعدي اين مكعب عبارت است از مجموعهي نقاطي كه دو مختص آنها 0 يا 1 و دو مختص ديگر بين 0 و 1 تغيير ميكنند. مثلاً![]() يك وجه دو بعدي اين مكعب است.
يك وجه دو بعدي اين مكعب است.
اين مكعب داراي 24 وجه دو بعدي است. [چرا؟]
وجه سه بعدي مكعب: وجه سه بعدي مكعب عبارت است از مجموعهي نقاطي كه يك مختص آنها 0 يا 1 و سه مختص ديگر بين 0 و 1 تغيير ميكنند.
مثلاً![]() يك وجه سه بعدي اين مكعب است. اين مكعب 8 وجه سه بعدي دارد.
يك وجه سه بعدي اين مكعب است. اين مكعب 8 وجه سه بعدي دارد.
در شكلهاي زير مكعب واحد چهاربعدي و چگونگي ساختن آن را با استفاده ازمدل گستردهاش ملاحظه ميكنيد:


سخن آخر اين كه يكي از كاربردهاي مهم اين فضا در معرفي فضاي مينكوفسكي در نظريه ي مشهور نسبيت مي باشد .
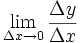
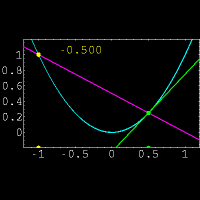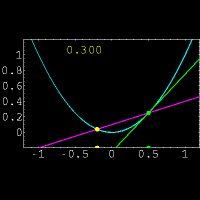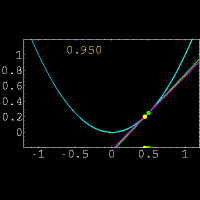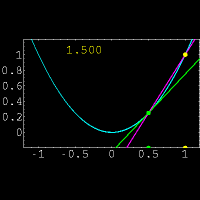
 نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند: 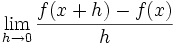
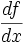 یا یا 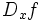 یا یا 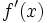 |
 |
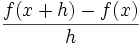
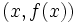 و
و 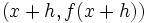 حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ،حاصل حد زیر است:
حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ،حاصل حد زیر است: