دنباله فیبوناتچی
 |
در سال 1202 لئونارد فیبوناچی (Leonardo Fibonacci) توانست به یک سری از اعداد دست پیدا کند که بعدها بعنوان پایه برای بسیاری از رابطه های فیزیک و ریاضی استفاده شد، کافی است از عدد صفر و یک شروع کنید. آنها را کنار هم بگذارید و عدد بعدی را از جمع کردن دو عدد قبل بدست آورید، بسادگی به این رشته از اعداد خواهید رسید :
0,1,1,2,3,5,8,13,21,34,55,89,144 ...
البته برخی از ریاضیدانان عدد صفر را جزو رشته فیبوناچی نمی دانند و یا حداقل آنرا جمله صفرم سری می دانند. نکته ای که تعجب برانگیز است آنکه اگر از عدد سوم نسبت اعداد این سری را به عدد قبلی حساب کنیم خواهیم داشت :
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
و یا :
1, 2, 1.5, 1,666, 1.6, 1,625, 1.6153, 1.6190, 1.6176, 1.6181, 1.6179و ...
بله بنظر می رسد که این رشته به سمت همان عدد طلائی معروف میل میکند. بگونه ای که اگر نرخ عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد 1.618033988749895 می رسیم که با تقریب 14 رقم اعشار نسبت طلایی را نشان می دهد.
بعدها محاسبات و استدلال های ریاضی نشان داد که این سری همگرا به سمت نسبت طلایی می باشد و جمله عمومی آنرا باتقریب می توان اینگونه نمایش داد :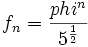 
که در آن Phi عدد طلایی میباشد. البته فرمول های دقیق دیگری وجود دارند که اعداد سری و یا اعداد بعدی (Successor) این سری را نمایش می دهند که دراین مطلب به آن نخواهیم پرداخت.
معمای زاد و ولد خرگوش
در واقع فیبوناچی در سال 1202 به مسئله عجیبی علاقمند شد. او می خواست بداند اگر یک جفت خرگوش نر و ماده داشته باشد و رفتاری برای زاد و ولد آنها تعریف کند در نهایت نتیجه چگونه خواهد شد. فرضیات اینگونه بود :- شما یک جفت خرگوش نر و ماده دارید که همین الآن بدنیا آمده اند.
- خرگوشها پس از یک ماه بالغ می شوند.
- دوران بارداری خرگوشها یک ماه است.
- هنگامی که خرگوش ماده به سن بلوغ می رسد حتما" باردار می شود.
- در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده بدنیا می آورد.
- خرگوش ها هرگز نمی میرند.
حال سئوال اینجاست که پس از گذشت یکسال چه تعداد خرگوش نر و چه تعداد خرگوش ماده خواهیم داشت؟
لئوناردو فیبوناچی ایتالیایی حدود سال 1200 میلادی مساله ای طرح کرد : فرض کنید که یک جفت خرگوش نر و ماده در پایان هر ماه یک جفت خرگوش نر و ماده جدید بدنیا بیاورند ... اگر هیچ خرگوشی از بین نرود , در پایان یک سال چند جفت خرگوش وجود دارد؟؟؟
فیبوناچی تصمیم گرفت برای محاسبه تعداد انها Fn را تعداد جفتها در شروع ماه N ام فرض کند.
پس F1 =1 و F2 =2 خواهد بود ... چون در شروع ماه اول فقط یک جفت اصلی وجود دارد...اما با شروع ماه دوم جفت اول جفت دوم را درست میکند.
سپس او متوجه شد که با شروع ماه N ام جفتها به دو گروه تقسیم میشوند: Fn-1 تعداد جفتهای قدیمی و تعداد جفتهای جدید پس از N-1 ماه است .چون جفت جدید پس از یک ماه تولید میشود و بعد از یک ماه دیگر اولین جفت خود را تولید میکند ... تعداد جفتهای جدید برابر تعداد جفتهای دو ماه قبل است که با Fn-1 نشان داده میشود .
پس :
Fn= Fn-1 + Fn-2
با استفاده از این فرمول و مقادیر اولیه F1 =1 و F2 =2 میتوان تعداد جفتها را پس از یک سال بدست اورد و نوشت F12=233 .
با یک توافق عمومی مقادیر اولیه از 1 و 1 بجای 1و 2 شروع میشود (بطوری که جمله های دنباله بصورت زیر نوشته میشوند)
... ,1,1,2,3,5,8,13,21,34,55,89,144,233
پس پاسخ این سئوال را در ابتدای مطلب بیان کرده بودیم.
مارپیچ فیبوناچی
 |
به شکل اول نگاه کنید و ببینید که به چه زیبایی از کنار هم قرار دادن تعدادی مربع می توان رشته فیبو ناچی را بصورت هندسی نمایش داد. حال اگر در هر یک از این مربع ها از نقاط قرمز ربع دایره هایی رسم کنیم در نهایب به نوعی از مارپیچ حلزونی شکل می رسیم که به مارپیچ فیبوناچی (Fibonacci Spiral) معروف می باشد. بدیهی است که نرخ رشد و باز شدن این مارپیچ متناسب با نرخ بزرگ شدن اعداد در سری فیبوناچی می باشد.
سری فیبوناچی چه در ریاضیات چه در فیزیک و علوم طبیعی کاربردهای بسیار دیگری دارد، ارتباط زیبای فاصله های خوش صدا در موسیقی، چگونگی تولد یک کهکشان و ... از جمله این کاربردهاست.
که دارای 
راس باشد که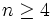
و یکی از رئوس از درجه ی 
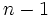و بقیه از درجه ی سه باشند، را یک گراف چرخ می نامیم- مانند مثال های زیر: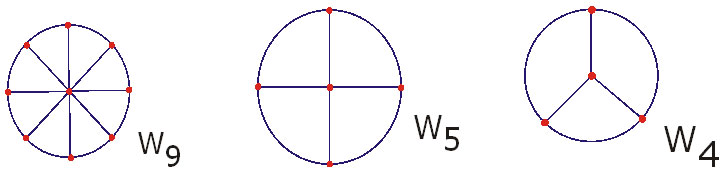 
نمایش می دهیم. 